AR1
Time Series analysis: AR(1) process
自回归过程
考虑
其中,随机干扰项
序列的稳定性由决定
一般地,考虑序列值
其中,
一阶自回归过程AR(1)
一阶自回归表达式:
其中,
求方差得:
根据上得出:
对(1)两边同时乘以
即:
根据
将k带入求得
即:
自相关系数只与间隔(k)有关,因此是平稳(stationary)的。
模拟过程
对于不同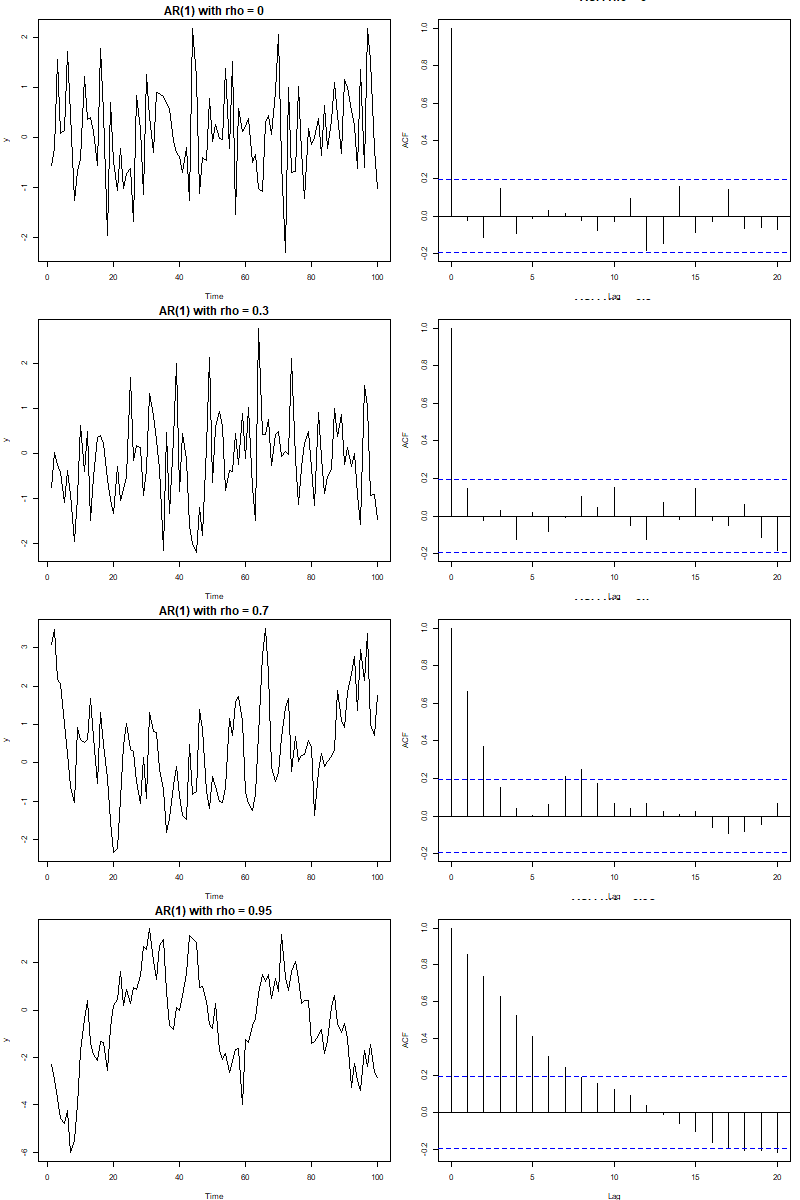
代码:
1 | set.seed(123) |
根据上图,自相关系数越小,ACF衰减越快,相反,ACF衰减越慢。
考虑
其中,随机干扰项
序列的稳定性由决定
一般地,考虑序列值
其中,
一阶自回归表达式:
其中,
求方差得:
根据上得出:
对(1)两边同时乘以
即:
根据
将k带入求得
即:
自相关系数只与间隔(k)有关,因此是平稳(stationary)的。
对于不同
代码:
1 | set.seed(123) |
根据上图,自相关系数越小,ACF衰减越快,相反,ACF衰减越慢。